-

-
adaptation
In relation to a complex adaptive system, adaptation is a process by which “experience guides change in the system’s structure so that as time passes the system makes better use of its environment for its own ends”.
In a biological context, an adaptation is a phenotypic trait that increases an individual's or group's fitness in a particular environment. The process of adaptation occurs via modifications of the genotype or behavior of an individual or group.
-

-
adaptive walk
A term used to describe a trajectory of changes undergone by a system to better operate in a given environment. In the context of a fitness landscape, each change can be seen as a step that either improves the performance of the system (higher elevation within landscape) or degrades the performance of the system (lower elevation within the landscape). See also fitness landscape.
-

-
agent-based model
A computational simulation in which the individual components ("agents") of a system are represented and interact explicitly. An agent-based model is typically iterated over time steps, with aspects of the agents updated at each time step. Agent-based models can be contrasted with models in which the behavior of the system is based on equations and individuals are not represented explicitly.
-

-
anthropic principle
The anthropic principle seeks to explain why the constants of the universe are consistently in the very fine band of possibilities in which life – specifically conscious life – could occur. The 'strong' anthropic principle places a purpose to the universe: to host conscious life. The 'weak' anthropic principle instead says that the observations being made by conscious beings are necessarily occurring in the very limited set of universes which are hospitable to life.
-

-
arms race
A term coined from the era before the first World War, representing a reinforcing (i.e. positive) feedback loop between two nations seeking to have the larger armed forces. The most well known arms race is the nuclear arms race of the Cold War.
In the modern era, the term has begun to describe competitions in which there is no definite goal beyond staying ahead of one's competitor. The term is often applied in biology, as in the description of the co-evolution of hosts and parasites or pathogen response to antibiotics.
An evolutionary arms race refers to the competition between two evolving populations to outperform each other. This is an analogy to a literal arms race such as the nuclear arms race between the Soviet Union and United States during the cold war. An example of this would be the rough-skinned newt (Taricha granulosa) evolving an increasingly strong toxin to protect itself from predation while the common garter snake (Thamnophis sirtalis) continues to evolve a resistance to the toxin.
-

-
artificial intelligence
Artificial intelligence (AI) is a branch of computer science concerned with the study and design of intelligent agents, often made to emulate human thought or decision making. Agents may be designed to perform tasks such as game playing, optimization, problem solving, modeling social behavior, and many others.
-

-
artificial life
Artificial life is a field of study that examines life and life-like systems through the use of computer, mechanical, and chemical models. Some topics of interest in the field include but are not limited to the origin of life, what life is and could be, self-organization, self-replication, and evolution.
-

-
attractor
In dynamical systems, an attractor is a value or set of values for the variables of a system to which they will tend towards over enough time, or enough iterations. Examples include fixed-point attractors, periodic attractors (also called limit cycles), and chaotic (also called "strange") attractors.
Limit points are points in the phase space or state space of a system. There are three kinds of limit points: attractors, repellers, and saddle points. A system will tend toward an attractor, and away from a repeller, similar to the way in which a ball rolling across a smooth landscape will roll toward a basin and away from a hill. A saddle point is so-named because it resembles an equestrian saddle. It therefore functions as an attractor to systems originating in "higher" regions, and as a repeller to systems originating from "lower" regions.
-

-
autocatalysis
The process of self-generated change. Most frequently it is a system of chemical reactions such that each reaction is aided (catalysed) by the product of another in a closed and self-perpetuating sequence.
-

-
autopoiesis
Literally, 'self-creation'. This describes a process by which a system creates and maintains itself. The term was coined by Humberto Maturana and Francisco Varela in the context of self-maintaining chemical systems.
-
-
basin of attraction
Within the phase space of a system, a basin of attraction (with respect to a given attractor) describes all the possible values for the system variables that will cause the system to tend toward a given attractor. This is similar to the way that all the surface water in a drainage basin will flow toward the point of lowest elevation. See also attractor.
-
-
betweenness centrality
In graph theory or network theory, this term denotes the number of shortest paths between all pairs of nodes that pass through a given node in a graph or network.
-

-
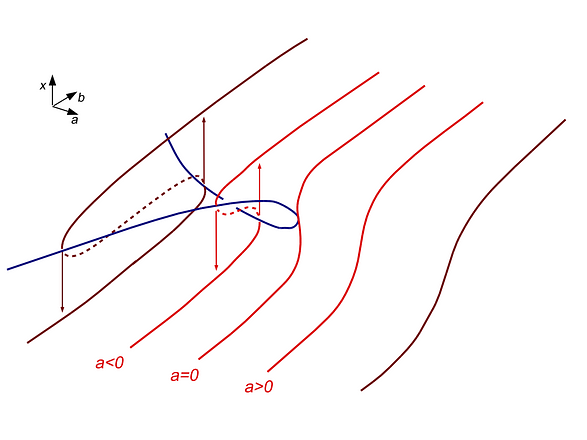
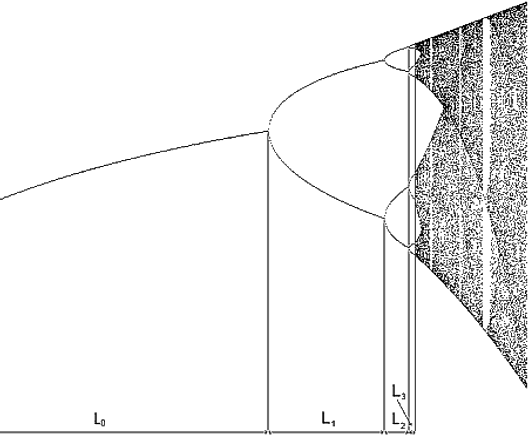
bifurcation
A change or branching of the qualitative properties of a dynamical system. For example, in the logistic map, the behavior of the system repeatedly bifurcates as the growth parameter ("R") increases. The bifurcations correspond to period-doublings in periodic attractors of the system.
-
-
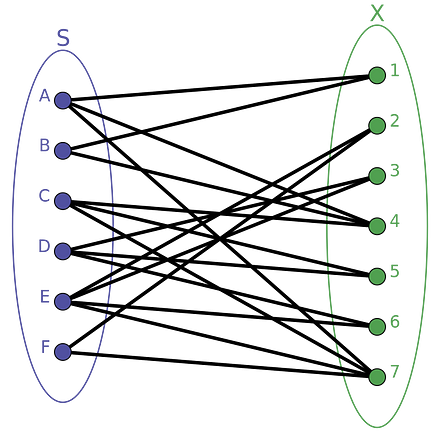
bipartite graph
Graphs that can be broken down into two disjoint sets of nodes, where edges may link nodes between two sets but not within a set. For example, imagine a graph of red and blue nodes, in which a red node can be connected to one or more blue nodes (and vice versa) but not nodes of its own color. Often useful for visualizing attributes of a population (e.g., the distribution of ethnic group memberships for individual people in a social network).
-

-
canalization
In evolutionary or developmental biology, the term "canalization" refers to the ability of a population or species to produce the same phenotype in successive generations in spite of significant change in its environment or its genotype. The term "canalization" was coined by the British biologist C. H. Waddington. See also robustness.
-
-
catastrophe theory
In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of general singularity theory in geometry. Small changes in certain parameters of a nonlinear system can cause equilibria to appear or disappear, or to change from attracting to repelling and vice versa, leading to large and sudden changes of the behaviour of the system. However, examined in a larger parameter space, catastrophe theory reveals that such bifurcation points tend to occur as part of well-defined qualitative geometrical structures.
-
-
cellular automaton
A mathematical or computational system in which simple elements ("cells") are arrayed in a regular lattice. At a given time step, each cell is in some discrete "state" (e.g., 0 or 1), and at each time step, each cell updates its state using a function of its current state and the states of its neighboring cells. To define a particular cellular automaton, one must specify the dimensionality of the lattice, the neighborhood of a cell, the set of possible states, and the state update function used by each cell. Plural is "cellular automata".
-
-
chaos
A phenomenon seen in dynamical systems, in which the system's future behavior is highly sensitive to the initial conditions of the system. See also butterfly effect.
-

-
Church-Turing thesis
The Church-Turing thesis states that any function that is "computable" --- that is, that can be computed by an algorithm --- can be computed by a universal Turing machine (invented by Turing) or, equivalently, by the lambda calculus (invented by Church).
-

-
clustering coefficient
In graph theory and network analysis, the clustering coefficient measures the degree to which nodes exist in tightly connected groups. More specifically, the "clustering" of a node measures how many of its neighbors are also linked to one another, and the clustering coefficient of a network is the average of the clustering of each of its nodes.
-

-
complex system
A system composed of a large number of interacting components, without central control, whose emergent "global'' behavior—described in terms of dynamics, information processing, and/or adaptation —is more complex than can be explained or predicted from understanding the sum of the behavior of the individual components. Complex systems are generally capable of adapting to changing inputs/environment and in such cases sometimes referred to as complex adaptive systems.
-

-
convergence
Convergence (in evolutionary computing) is a means of modeling the tendency for genetic characteristics of a population to stabilize over time. Convergence (in logic) refers to the property in which different sequences of transformations of the same state terminate at the same end state, independently of the path taken (they are confluent). Basically, it's when variables come together producing an emergent phenomenon.
-

-
critical phenomena
Critical phenomena refers to study of critical points in phase transitions. The melting, sublimation, and boiling curves between the phases of a typical substance represent the critical points for the phase transitions.
-
-

-
deterministic dynamics
Determinism refers to mathematical models where the state at t+1 is absolutely determined by the state at time t. Deterministic dynamics refers to a simplified fluid model in which the dynamics are set by a fixed number of fluid equations. There is no probabilistic element in deterministic dynamics.
-
-
differential equation
A continuous differential equation relates the derivative of one or more variables with the current state and derivatives of itself or other variables. These could be used to describe how the system is changing based on how it has been changing and the state it is in. Equations like these have been used to describe fluid dynamics, populations, or any system in which change is itself dependent upon the state and previous flow of the system.
-
-
dimension
The general notion of dimension can be thought of as the number of different coordinates needed to specify a point distinctly from any other point. In the framework of a fractal dimension, dimension relates the logs of the rate of change of a measurable aspect of a fractal pattern as it is iterated.
The Hausdorff (or Hausdorff-Besicovitch) Dimension is a metric that can be used to calculate a fractal dimension of an object and is generalized as N = S^D. In this formulation, N is the number of pieces an object can be divided up into equally that have the same appearance as the original object (i.e. a square being divided up into smaller squares.) S is the scale of N in relation to the larger object (i.e. when the parts of a 4x4 square are made into 16 1x1 smaller squares, the smaller pieces in relation to the whole object is said to have the scale factor of 4, or S of 4). Finally, D is the dimension of the object, which operates with the scaling factor, in the manner of S^D, to describe how the length, area, and volume change as the object shrinks or gets larger. When calculating fractal shapes D is solved for by taking the natural logarithm of N and dividing it by the natural logarithm of S: D = ln N / ln S.
-
-
directed graph
A graph where relationships between nodes, represented by edges, has the added constraint of how nodes may interact. This is often indicated on a graph by adding arrows to edges.
-
-
discrete time
The assumption used in some models (either mathematical or computational) that time is divisible into discrete "steps"; a system's state is updated at each discrete time step in the model. Working with mathematical functions (maps) in discrete time potentially can yield markedly different behavior when compared to the equivalent function in continuous time.
-

-
dissipative structure
A dissipative structure is an organized structure in open systems which are operating far-from-equilibrium exchanging
energy and matter with outside environment. A dissipative system is characterized by the spontaneous appearance of symmetry breaking and the formation of complex, sometimes chaotic, structures.A whirlpool is a dissipative structure requiring a continuous flow of matter and energy to maintain the form.
-

-
dynamical system
A system that is described by temporal change of a point in a state space (or phase space). At any given time, the system is in a particular state in its space, and it follows an evolution rule that describes how the system changes states over time. Generally, a continuous dynamical system will be described by differential equations, while a discrete dynamical system will be described by difference equations. Stochastic dynamical systems will have solutions related to a probability distribution, while deterministic dynamical systems will have exact solutions.
-

-
embodied cognition
Embodied cognition, such as the work of Barsalou on perceptual symbol theory, is a view of cognition that grounds all symbolic activity in the experiences of the body. For example, to understand the concept 'chair', we partially activate all recorded experiences of 'chair', building an abstraction of chair from recent and distant experiences.
-

-
emergence
A process by which a system of interacting subunits acquires qualitatively new properties that cannot be understood as the simple addition of their individual contributions.
-

-
entropy
Entropy, in the thermodynamic sense, is the tendency of a system to move from a more ordered state to a less ordered state. In Boltzmann's statistical mechanics, the notion of "order" and "disorder", and thus the definition of entropy, corresponded to the number of possible microstates corresponding to a given macrostate. In information theory, Shannon entropy and Hartley entropy measure the distribution of discrete states in a system. A uniform distribution would have maximum entropy. Shannon entropy measures frequencies of states, while Hartley entropy ignores frequency and only examines the presence of states (out of all possible states).
-

-
equilibrium
Equilibrium, meaning balance, occurs when all forces or influences on a system are balanced. In physics an example is when the sum of forces on an object result in no change in motion. In dynamical systems, an equilibrium is a solution or behavior of the system that does not change over time (a "fixed point" or "steady state").
-

-
ergodic process
A stochastic process such as a random walk can take on different "realizations" (where each realization has a particular initial condition and a particular sequence of steps). A stochastic process is said to be ergodic if its average behavior over one (sufficiently long) realization is equivalent to its average behavior over all possible realizations. A key reason to consider whether a process is ergodic is to determine if, given enough time, the process passes through all possible states with equal probability. If it so, the ultimate behavior of the process is not dependent on the initial conditions.
-
-
evolvability
Evolvability describes the capacity of a system to undergo adaptive evolution. Evolvability is the ability of a population of organisms to not merely generate genetic diversity, but to generate adaptive genetic diversity, and thereby adapt via natural selection.
-
-
Feigenbaum’s constants
Universal ratios discovered from bifurcation patterns occurring in one-dimensional function maps (such as the logistic map) with a single quadratic maximum, or 'hump'. The bifurcations relate to phenomena with oscillatory (cyclic) behavior, such as swinging pendulums or heart rhythms. The most well-known one, Feigenbaum's Delta, refers to the spacing between parameter values required to double the cycle's length, which decreases exponentially by a factor approaching approximately 4.669. The slightly less well-known Feigenbaum's Alpha refers to the scaling factor by which the x-values decrease for each periodic doubling on said function map, which approaches approximately 2.503.
-

-
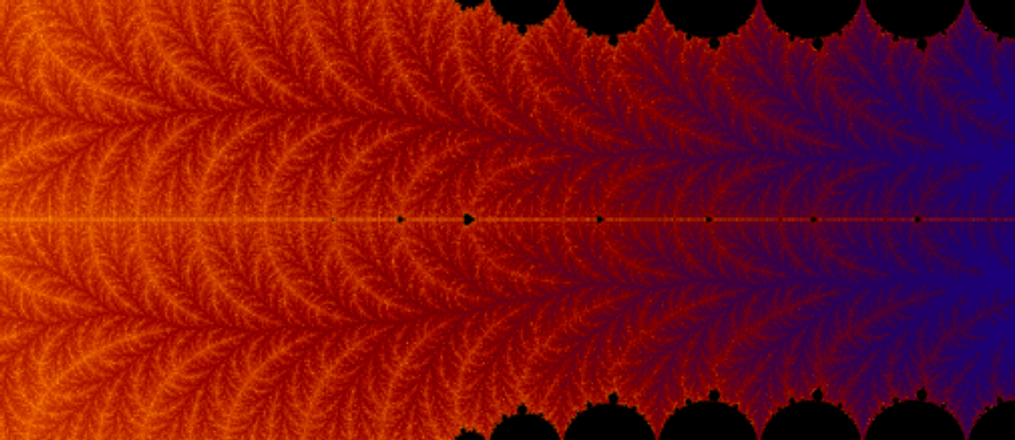
fitness
Fitness is the relative success in transmission of a variant among a population. Most commonly used in biology, fitness refers to reproductive success (or survival) of individuals of a given genotype or phenotype. Extending to cultural evolution, fitness may refer to the combination of factors that influence whether "memes", beliefs, ideas, practices, etc. will spread within a population.
-
-
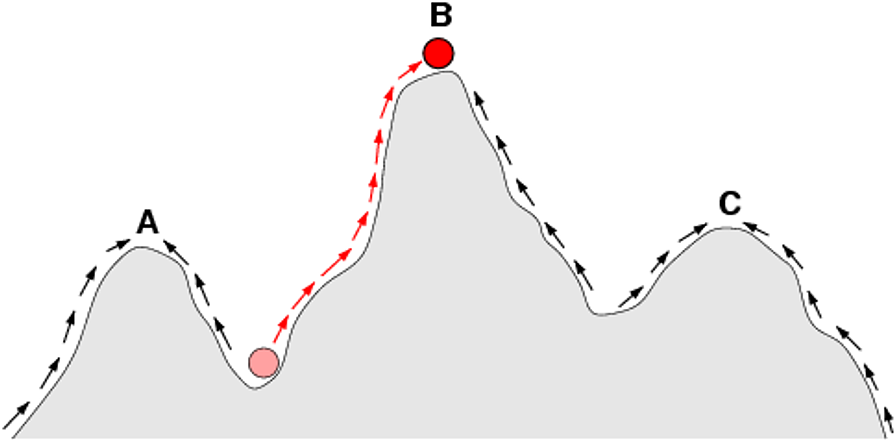
fitness landscape
An n+1-dimensional function, or surface, used to visualize fitness over an n-dimensional trait space. The height of the surface at each point gives a fitness measure for a particular set of values for the traits of interest. Peaks and valleys in the surface represent local maxima and minima in the landscape.
-
-
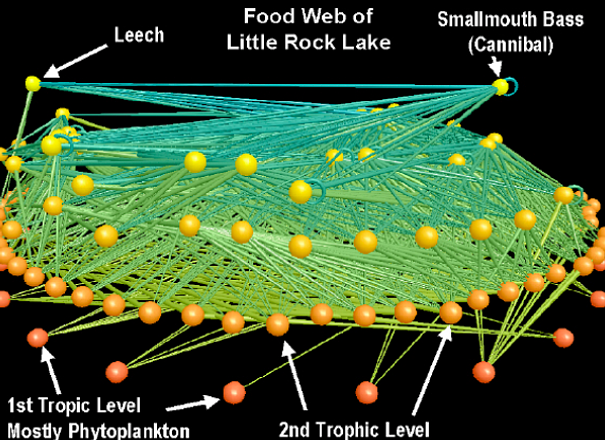
food web
Network of organisms from selected ecosystems, typically representing predator-prey (or more generally, trophic) relationships between species of interest. Wolves, for example, might be linked to deer (since wolves prey on deer), who are in turn linked to the local vegetation.
-

-
fractal
A geometric object or shape which exhibits self-similarity across scales. See also fractal dimension.
-

-
fractal dimension
The term fractal dimension was originally used synonymously with Hausdorff dimension, but later grew to represent a general measure of how quickly length, area, or volume change with decreasing scale. The fractal dimension is not necessarily an integer quantity, meaning it can be a fractional value.
-

-
Game of Life
Conway's Game of Life (by British Mathematician John Conway) is a two-dimensional cellular automaton with a simple set of rules. At a given time step, a cell is in one of two states: alive or dead. The state of a cell at the next time step is a function of its current states and the states of cells in its Moore neighborhood (the surrounding 8 cells). The rules of Life are: 1) live cells with fewer than two live neighbors die (underpopulation); 2) live cells with more than three live neighbors die (overpopulation); 3) dead cells with exactly three live neighbors become alive (reproduction); 4) all other cells do not change state. Despite the apparent simplicity of the individual cells' behavior, the cellular automaton can exhibit elegant, complex patterns over time. A wide variety of patterns can be achieved, with the user varying only the initial configurations of the cells.
-
-
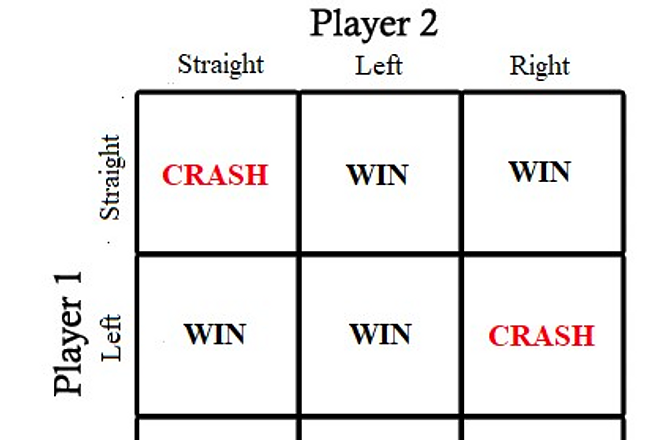
game theory
The mathematical study of decision making in situations of cooperation or conflict with multiple actors, each trying to maximize their own gain or utility.
-

-
genetic algorithm
Genetic algorithms are a family of computational search and learning methods inspired by biological evolution. Evolution takes place on a population of individuals, each of which represents a candidate solution to a given problem. At a given generation, each individual's fitness is calculated according to a user-defined fitness function. A selection process probabilistically chooses the fittest individuals to reproduce (with variation resulting from crossover and mutation); their offspring make up the next generation. The algorithm runs for either a fixed number of generations, or until an individual is found whose fitness is above a user-defined threshold.
-
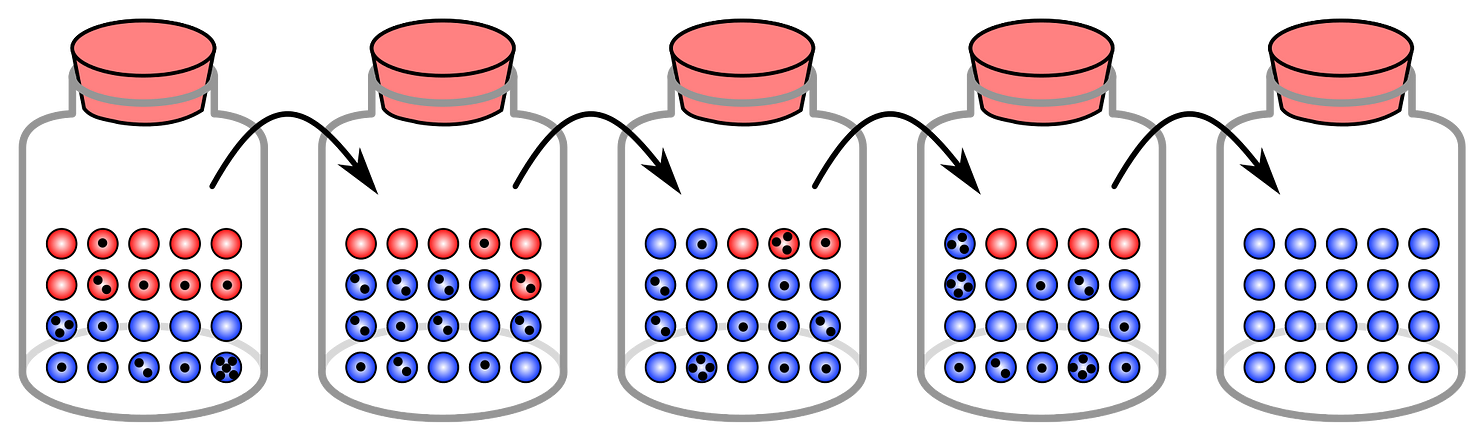
-
genetic drift
Genetic drift is the change in allele frequencies for a gene from one generation to the next due to random sampling events in a population. This is different from selection, where allele frequencies change because of a variation in reproductive fitness associated with each allele.
-

-
homeostasis
Homeostasis refers to the ability of an organism or other system to maintain a stable internal environment, even as its external environment changes. This is often important for regulating the continued function of the system, and usually employs balancing feedback mechanisms (for example, burning available calories to maintain body temperature in cold weather).
-

-
hypercycle
A category of autocatalytic or self-replicative biochemical reaction networks where the constituents in the network act as catalysts for the production of other constituents (themselves catalysts) in the network. In addition, each constituent is able to instruct its own production, and is therefore autocatalytic. Hypercycles, which are a novel class of cyclic networks with nonlinear reaction kinetics, provide a principle and a mechanism for self-organization because they allow the evolution of a set of functionally coupled self-replicative entities.
-
-
hysteresis
A property of dynamical systems in which different stable states can co-exist depending on both the system's history and current trajectory.
-
-
information theory
Information theory is theory concerned with mathematical analysis of unpredictability in a system (quantified as "Shannon entropy") and its applications to communication and other models of information storage and transmission.
-

-
isomorphism
Isomorphism refers to the similarity between two systems or two processes such that the defined patterns of relations/operations among each system's elements are perfectly analogous and map neatly one-to-one between the systems, at some level of coarse graining. For example, two dynamical systems may be considered isomorphic if they can be represented with the same set of differential equations. Recognizing isomorphisms between analogous phenomena (such as bird flocking and fish schooling) allows prediction of the dynamics of both systems with the same general model.
-
-
keystone species
A keystone species is one that plays an important role in the composition or structure of its ecosystem for some reason other than abundance. If this species were removed, the ecosystem would become unstable and possibly collapse. For example a predator may be necessary to control the population size of its prey.
-

-
L-system
A formal grammar that recursively outputs symbols and strings of symbols based on a set of production rules in order to represent geometric shapes and patterns. An initial symbol or string is used as a seed to create a new string; this new string is then used as the seed for the next group of symbols. Symbols representing line length, line angle, and scale can be used to easily represent geometric patterns that are fractal. L-systems are named after the botanist Aristid Lindenmayer who pioneered their development and used them to categorize the algorithmic structure of plants.
-
-
limit cycle
A limit cycle is a trajectory in a dynamical system that repeats itself (i.e., is cyclical, or periodic) and that is an attractor for at least one neighboring trajectory.
-
-
link
A link can be thought of as a connection, relation, or association that when represented graphically illustrates a pathway with an origin and endpoint, referred to as a 'node' or a 'vertex'. Also called 'edges' and 'arcs', links can be directed or undirected.
-
-
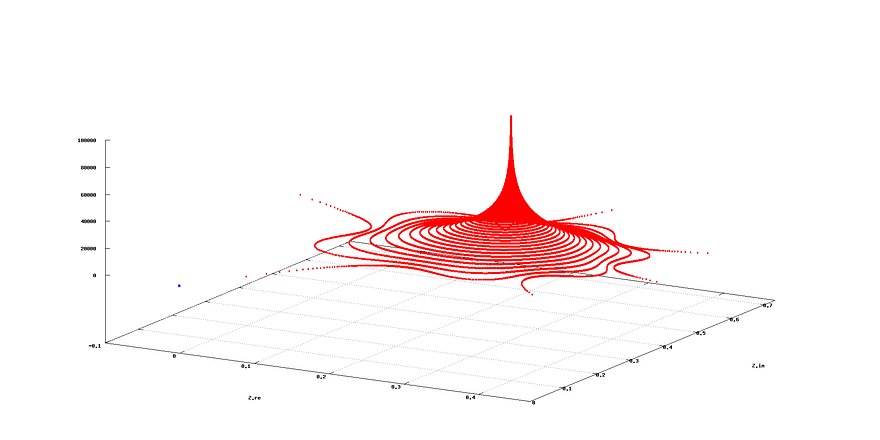
logistic map
The logistic map is the simple recurrence relation: x_(n + 1) = x_n * R * ( 1 - x_n ), which produces chaotic behavior under certain parameters .
This map is a version of Verhulst's logistic model of population growth, where x_n represents the population (as a fraction of carrying capacity) at time n, and R is the growth rate. In order to keep x_n between 0 and 1, R is restricted to be between 0 and 4.
-
-
long-tailed distribution
A statistical distribution characterized by a skewed, or a slow-decaying, tail of extreme values. Such distributions are often contrasted with Normal (Gaussian) distributions, which do not have skewed tails. The significant weight of these extreme values in the population skew the mean away from 'typical' values in both median and mode. In some cases, long-tailed distributions are characterized by power laws. In the context of complex networks, long-tailed distributions are commonly found in a network's degree distribution.
-
-
Lyapunov exponent
The Lyapunov exponent is a value that describes the rate at which two nearly identical trajectories within a dynamic system's phase space will separate from one another per unit of time. It is indicative of a system's sensitivity to initial conditions: a large Lyapunov will reflect a system in which a very small perturbation of the system will cause a large change in the trajectory of the system within its phase space.
For N-dimensional systems, there will be N Lyapunov exponents, one that measures the rate of separation along each dimension. The largest of these is called the "maxiumal Lyapunov exponent" or MLE. A positive MLE is one indicator that a system is chaotic.
-
-
Markov chain
A random process that undergoes transitions from one state to another, in which the probability distribution of the next state depends only on the current state and not on the sequence of events that preceded it.
-
-
maximum entropy
The principle of maximum entropy states is based on the premise that when estimating the probability distribution, one should select that distribution which leaves the largest remaining uncertainty (i.e., the maximum entropy) consistent with the constraints. That way, no additional assumptions or biases have been introduced into the calculations.
-
-
natural selection
The disproportionate propagation of heritable characteristics that are advantageous for the system
-

-
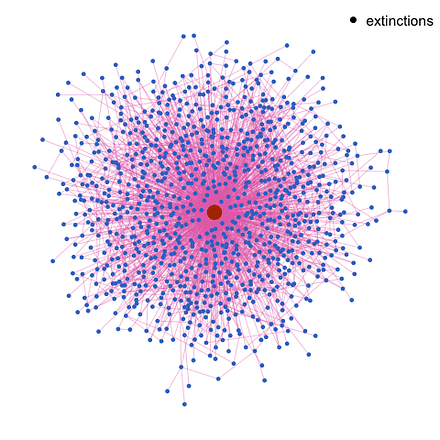
network
A network (or graph) is a collection of elements, called vertices or nodes, connected by edges or links. Edges typically are either one-way or two-way connections. A network is often represented by an adjacency matrix.
-
-
-
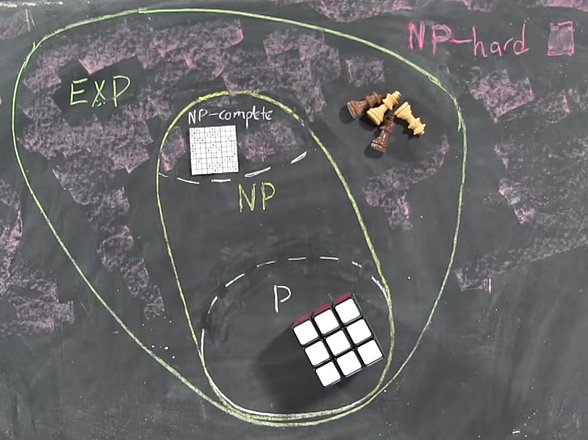
NP
Refers to the class of nondeterministic polynomial time problems: those for which there is no known polynomial-time algorithm to solve the worst-case instances, but for which there is a polynomial-time algorithm to verify whether a candidate solution to a problem instance is indeed a solution. See also P.
-
-
NP-complete
An NP-complete problem is one that is (1) in NP and (2) any other problem in NP can be translated, in polynomial time, into an instance of the given NP complete problem.
-

-
P
Refers to the class of polynomial time problems: those for which every instance can be solved in polynomial time (with respect to the size of the input). See also NP.
-

-
Pareto optimality
A situation where no indivdual stands to gain further utility, whether in terms of money, energy, or some other asset, without doing so at the expense of another individual.
-
-
path dependence
Path dependence refers to the idea that current and future states, actions, or decisions depend on the sequence of states, actions, or decisions that preceded them---namely their (typically temporal) path. For example, the very first fold of a piece of origami paper will determine which final shapes are possible; origami is therefore a path dependent art.
-
-
phase space
A phase space is a multidimensional space that represents all possible states of a dynamical system. The dimensions of the phase space reflect the variables of the system. Each point in the phase space therefore represents a possible state of the system. See also state space.
-

-
phase transition
These are state changes in the underlying system - when you change the macroscopic variables of a system sometimes its properties will abruptly change, often in a dramatic way. These transitions may be reversible (such as the transitions between bear and bull markets or water freezing and thawing) or unidirectional (such as the development of Type II diabetes or combustion).
-
-
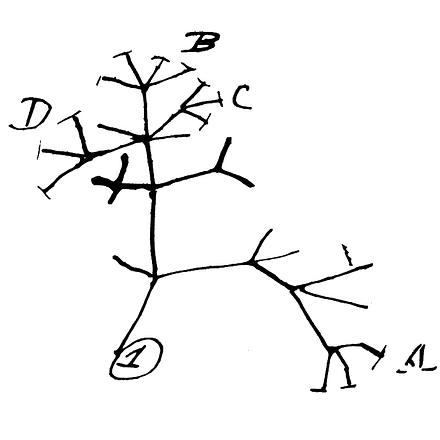
phylogeny
Phylogeny describes the evolutionary history of a gene, species, genus, or other evolutionary unit.
-
-
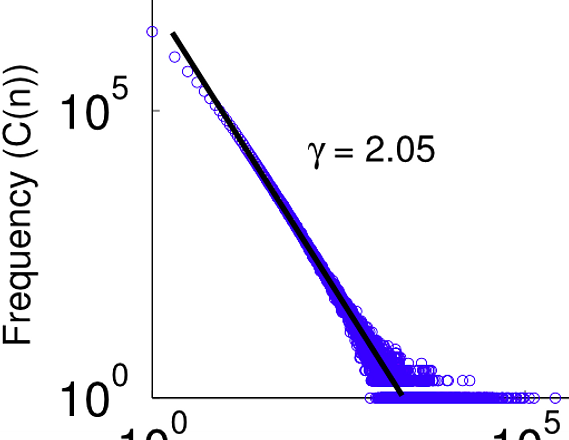
power law
A power law is a functional relationship between two variables of the form
. The degree distribution among nodes in growing scale free networks and other phenomena involving preferential attachment, such as continuously self-compounding acquisition proportionate to current assets, create power-law distributions.
-
-
principle of maximum entropy
The principle of maximum entropy states is based on the premise that when estimating the probability distribution, one should select that distribution which leaves the largest remaining uncertainty (i.e., the maximum entropy) consistent with the constraints. That way, no additional assumptions or biases have been introduced into the calculations.
-

-
random walk
A type of stochastic process in which an entity (e.g., a molecule, a animal, a stock price) follows a path consisting of a series of steps in random directions. For very small steps, a completely random walk approaches Brownian motion.
-

-
repeller
A repeller is one of the three types of limit points in the phase space of a dynamical system, with the other two being attractors and saddle points. Repellers have the effect of directing the trajectory of a system away from themselves within the phase space.
-

-
resilience
Resilience describes the ability of a system to persist and maintain its core functions and/or purpose in the presence of disturbances, stresses or other changes in its environment.
-

-
robustness
Robustness describes the ability of a system to maintain a certain behavior, trait, or characteristic regardless of changing environmental conditions. Robustness is often contrasted with optimization, especially in human-constructed systems. This is because the quality of being robust usually requires that one or more components of a system operate at sub-optimal levels in some situations in order to maintain the ability to operate acceptably at any level under most conceivable scenarios. Conversely, a system that is highly optimized typically operates very well under certain conditions but then becomes less than operational if those conditions change.
-
-
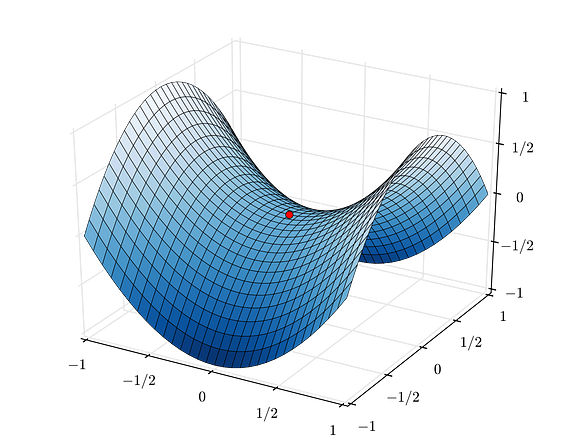
saddle point
A saddle point refers to a point in the phase space of a system that attracts the trajectory of a system when it originates from some directions, and repels the trajectory of a system when it originates from other directions. The name is derived from its resemblance to an equestrian saddle when the phase space is visualized in three-dimensional space.
-
-
scale-free network
A scale-free network is one that has a power-law degree distribution. Under such a degree distribution, the vast majority of nodes have low degree and only a small fraction of nodes (hubs) have high degree. Because of this property, scale-free networks tend to be robust to random node failure but vulnerable to targeted attacks upon hubs.
-

-
second law of thermodynamics
The second law of thermodynamics states formally that isolated systems always increase in entropy. This could be equivalently stated by noting that they trend towards a state of uniformity or equal mixing.
-

-
self-organization
Self-organization is a process in which pattern at the global level of a system emerges solely from numerous interactions among the lower-level components of the system. Moreover, the rules specifying interactions among the system’s components are executed using local information, without reference to the global pattern.
-

-
self-similarity
Self-similarity is a phenomena that occurs when the structure of a sub-system resembles the structure of the system as a whole, and then the structure of a sub-system within that sub-system resembles the structure of the larger sub-system, and so on. Self-similarity is the defining property of fractals.
-

-
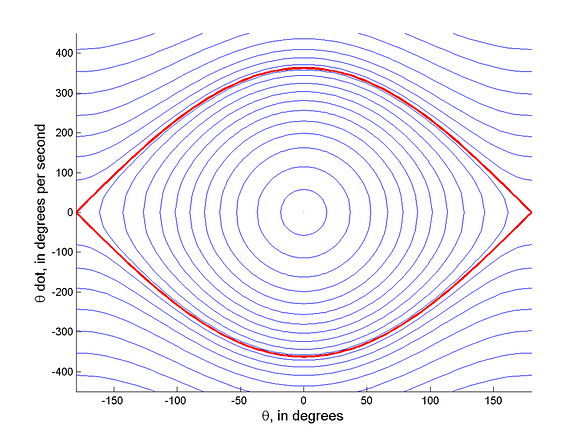
sensitive dependence on initial conditions
A system's sensitivity to initial conditions refers to the role that the starting configuration of that system plays in determining the subsequent states of that system. When this sensitivity is high, slight changes to starting conditions will lead to significantly different conditions in the future. Sensitive dependence on initial coditions is a defining property of chaos in dynamical systems theory.
-
-
Shannon information
Shannon information, described by mathematician Claude Shannon, is a measure of the unpredictability of a message, given a message source, communication channel, and reciever. This unpredictability, or entropy, relates to the sum of the probabilities of each element in the message. The higher the entropy, the more information that is present.
-
-
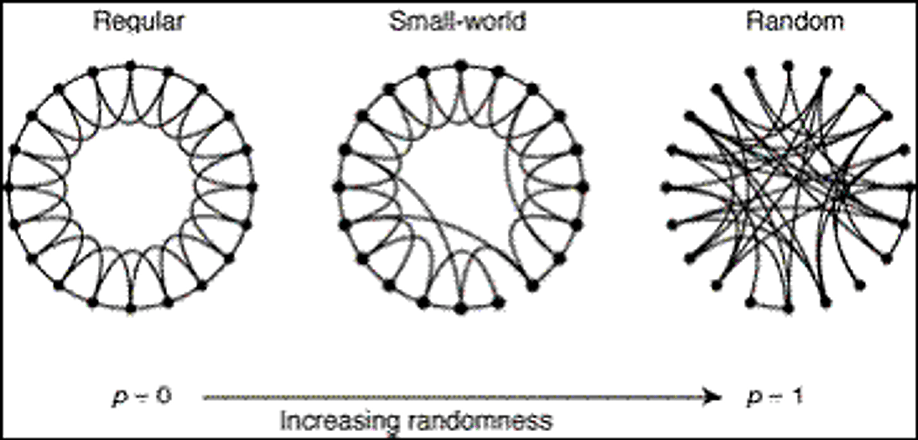
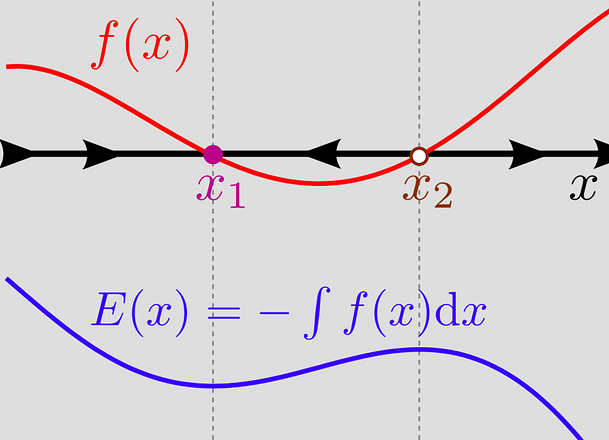
small-world network
A network in which most pairs of nodes are not connected, but there are a small number "long-distance" links that result in low average path length and a high clustering coefficient.
-
-
statistical mechanics
The field of statistical mechanics seeks to explain how macroscopic behaviors of a system emerge from the statistical properties of large numbers of "microscopic" components making up the system. Statistical mechanics was originally developed by Ludwig Boltzmann as a foundation for thermodynamics, but the ideas and techniques of statistical mechanics have since been applied in a large number of fields, ranging from physics to social sciences.
-
-
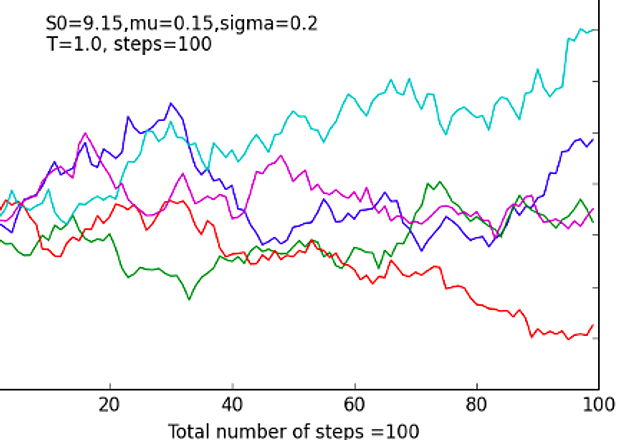
stochastic process
A stochastic process is process whose behavior (i.e., transition from one state of the system to a successor state) has random or probabilistic components. A classic example is a random walk.
-
-
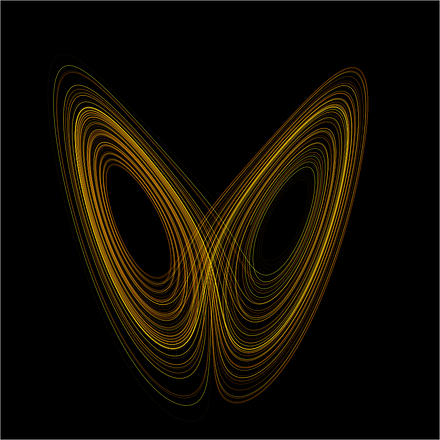
strange attractor
A strange attractor is a type of attractor that has fractal structure. Strange attractors most often occur in dynamical systems in regimes exhibiting chaos.
-

-
thermodynamics
Thermodynamics is a field of the natural sciences that focuses on the relationships among heat, energy, work and entropy.
-

-
time series
A time series is a set of sequential measurements taken at regular time intervals to indicate the change in the state of a system (i.e. its behavior) over time.
-

-
tipping point
Places where a small change in the input can dramatically affect the outcome.
The term is said to have originated in the field of epidemiology when an infectious disease reaches a point beyond any local ability to control it from spreading more widely. A tipping point is often considered to be a turning point. The term is now used in many fields to describe almost any change that is likely to lead to additional consequences. In the butterfly effect of chaos theory, for example, the small flap of the butterfly's wings that in time leads to unexpected and unpredictable results could be considered a tipping point.
-

-
tragedy of the commons
When a group of people share a resource, such as the original English commons of a town, each person has an incentive to use the resource but no incentive to restore the resource, sometimes resulting in a mentality that may ruin the shared resource for all. This is called the "tragedy of the commons".
-
-
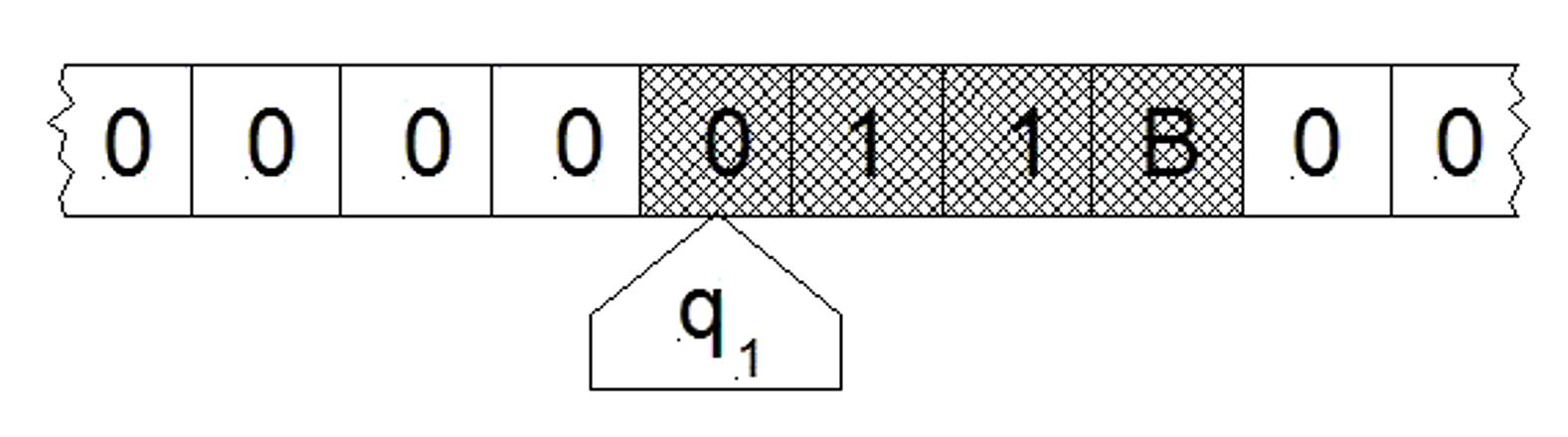
Turing machine
The British mathematician Alan Turing devised a hypothetical machine to carry out mathematical "algorithms". This construct is now termed a "Turing Machine". A given Turing machine consists of a linear "tape" containing readable/writable "cells", a "tape head" that can either read or write a symbol on the current tape cell or move to the left or the right on the tape, a set of "states" that the machine can be in at a given time, a initial state that the machine starts in, and a set of rules that map the current state and contents of the current tape symbol into an action for the tape head to take. The machine proceeds over a series of time steps until it reaches the "halt" state (if it is a "halting" machine). Turing's goal in devising this construct was to formalize the notion of "definite procedure" (or "algorithm"). A given Turing machine corresponds to what we would now call a "program" or "algorithm".
A universal Turing machine is a Turing machine that can emulate the operation of any other Turing machine on a given input. The universal Turing machine, designed by British mathematician Alan Turing, gave an early blueprint for programmable computers.
-
-
utility
The principle of utility posits that individuals will engage in actions or behaviors that maximize happiness or well-being. Theories based on rational choice assume individuals will attempt to maximize utility.
-
-
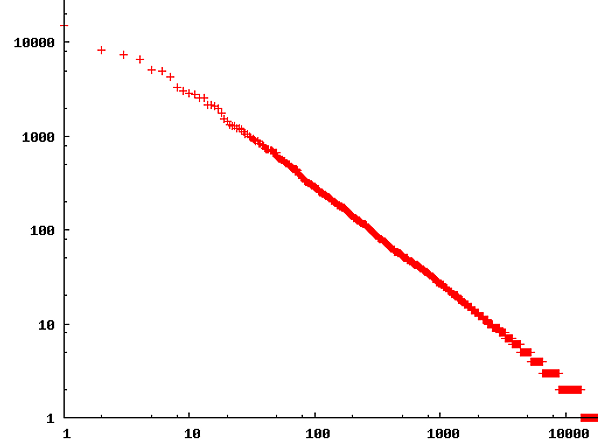
Zipf's law
Zipf's law is an empirical observation that, in certain systems, if values (e.g., word frequencies in a text) are ranked from most to least frequent, each value is inversely proportional to its rank in the list. The term originates from the name of the American linguist George Kingsley Zipf, who noted the phenomena in reference to the frequency distribution of words in any given language, and the fact that the frequency of each word is inversely proportional to its rank in the list. This same model has been applied to various types of data, such as the relative populations of different cities, the income rankings of individuals, and the size rankings of corporations.
