Complexity Explorer Santa Fe Institute

Ordinary Differential Equations

Enroll

Lead instructor: Elizabeth Bradley

Your progress is not being saved! Enroll now or log in to track your progress or submit homework.

10.1 Unit 3 Homework » Homework Part 3

Quiz scores are NOT recorded.

  • You may come back to quizzes and take them as many times as you like
  • When you are finished, clicking the "Score" button at the bottom of the test will show you the correct responses.

Instructions

(The following questions are refered to in the solutions video as Part A, Part B, Part C, Part D, and Part E of Question 3.)

As you observed in the previous two problems, forward and backward Euler both make errors. Combining the two of them, however, can be surprisingly effective. Implement a solver that averages a forward and backward Euler step:

\vec{x}(t+\Delta t)=\vec{x}(t)+\frac{\Delta t}{2}\bigg[f(\vec{x}(t))+f(\vec{x}{__F}{__E}(t+\Delta t))\bigg]

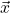Here \vec{x}{__F}{__E}(t+\Delta t) is the result of applying one step of the forward Euler algorithm starting from \vec{x} with time-step 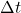\Delta t. This method averages the slope at that point with the slope at the originial point and uses that averaged slope to move forward. This is sometimes called the trapezoidal method in the literature.