- 16 Feb 2016
Anthony Rhodes, the instructor of Complexity Explorer’s Vector and Matrix Algebra tutorial, is currently finishing his PhD in mathematical sciences with an emphasis in machine learning. His current project focuses on situational computer vision, in which a computer algorithm is given an image and the algorithm is tasked with determining if it is an example of a complicated situation. For instance, if a computer is given an image with a dog, can it instantiate that this image is an example of a complicated situation like dog walking?
After finishing his doctoral work with Melanie Mitchell, Anthony is likely to head towards more work with artificial intelligence in the subfield of knowledge extraction. In this subfield, computers could learn using more abstract processes, for example learning through analogy. He has a natural ability to effectively communicate these complicated concepts and thus would be well suited for mix of academic work with teaching and research along with a mix of working in the tech industry on real-world applications. Look for him in a city like Seattle that has an Artificial Intelligence community with non-profit tech companies and universities working together.
Q: How is an understanding of vector and matrix algebra important for complex systems research?
Matrix Algebra has wide applicability, in fact most fields in the applied sciences use the language of matrix algebra. It is so fundamental that one might consider that if math is the language of science, then matrix algebra might be considered the vocabulary or alphabet of math. If you have an understanding of the basic language of matrices then you can encode real-world situations of complex systems using matrix algebra. From there, you can extract the structural information that is in the complex network. Once the network is represented as a matrix, it can be studied using the big theorems that are related to matrices, like eigenvalues, to further investigate the underlying structure to reveal information such as the shortest paths, connectivity and influential nodes in the network. Complex abstract networks can be turned into a matrix
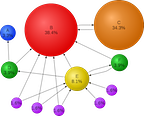and one can use matrix algebra to solve interesting problems. One well-known example of this type of application is Google’s famous PageRank algorithm which uses matrix representation of the network of webpages to determine which pages are most central to that network and thus are the most relevant to your search. Mapping technology also uses matrices to determine route efficiency via Dijkstra's algorithm. Anthony has some practical advice for achieving success in his Vector and Matrix Algebra tutorial
-
after watching a lecture, check your understanding by engaging a friend to see if you can succinctly explain the concept to them.
- connect with a community of students to discuss the topics using the language of the course to help solidify the concepts.
-
