Solution Gallery
Browse through top Challenge solutions from closed Challenges. Get inspired by the novelty and variety of approaches.
Hoping to participate in future Challenges? Understand how you can best frame and present your own solutions to present and future Challenges.
Are you from an organization thinking of partnering with the Santa Fe Institute to present your own Challenge? Get an idea of the breadth and quality of the solutions you might expect.
Spring 2018 CXC featured solutions
For Spring 2018's Challenge we've chosen to highlight the best video submission, written solution and tournament submission separately. To see the original challenge question and to watch all video submissions, click here.
Spring 2018 Written Submissions:
Click the winner's name to see their full paper.
1st Place: Sean Dougherty
 This writeup had an excellent set of references that helped explain and explore the problem in more depth. They used this previous literature, especially Axelrod’s work on the evolution of cooperation to identify a set of 27 potentially successful strategies for this Challenge, which they explored in depth. The ideas for future research were novel and involved examining the roles of signaling and exploring real-world implications of the model. The conclusion was very interesting showing that even perfect information is not very helpful in this game, and it contrasted these results to the previous literature in similar spaces.
This writeup had an excellent set of references that helped explain and explore the problem in more depth. They used this previous literature, especially Axelrod’s work on the evolution of cooperation to identify a set of 27 potentially successful strategies for this Challenge, which they explored in depth. The ideas for future research were novel and involved examining the roles of signaling and exploring real-world implications of the model. The conclusion was very interesting showing that even perfect information is not very helpful in this game, and it contrasted these results to the previous literature in similar spaces.
2nd Place: Victor Iapuscarta
 This writeup featured a very well written description of the Challenge itself, and drew on work in behavioral economics and complexity theory to explore the problem. The graphs were very helpful in illustrating the result, and they explore the role of meta-agents, i.e., agents composed of other agents. The strategy that they developed as a result of this analysis also wound up generating the best strategy in the tournament.
This writeup featured a very well written description of the Challenge itself, and drew on work in behavioral economics and complexity theory to explore the problem. The graphs were very helpful in illustrating the result, and they explore the role of meta-agents, i.e., agents composed of other agents. The strategy that they developed as a result of this analysis also wound up generating the best strategy in the tournament.
3rd Place: Muhammad Hijazy

This writeup excelled at drawing analogies between the Challenge and the stock market / financial system. The explanation of the problem was well done, and they also did a good job of defining what it mean to be successful, which included being stable, profitable, versatile, adaptive, and unpredictable. They then developed a number of different strategies that attempted to maximize these success functions in different ways. They also discovered that giving agents perfect information did not necessarily lead to better results, and concluded with a discussion of how the model might better take psychological and cultural factors into account
Honorable Mentions: Rohan Mehta, Simon Crase, Bernhard Geiger, Flavio Massimo Saldicco, Luís Gonçalo Dias de Calvao Borges
Spring 2018 Video Submissions:
Click on the winner's name to see their full video.
1st Place: Rohan Mehta
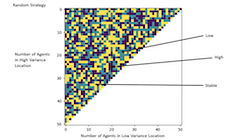 This video excelled at explaining the basic problem, and then quickly moved to defining the space of agents as strategies which took into account the number of agents in the low and high pools. It then took a unique look at the strategy space based on the notion of a Nash equilibium, i.e., can any agent do better by moving to a new pool. It then expanded on this notion by looking at cliques, or groups of agents that acted together. The graphics were very helpful in explaining the results.
This video excelled at explaining the basic problem, and then quickly moved to defining the space of agents as strategies which took into account the number of agents in the low and high pools. It then took a unique look at the strategy space based on the notion of a Nash equilibium, i.e., can any agent do better by moving to a new pool. It then expanded on this notion by looking at cliques, or groups of agents that acted together. The graphics were very helpful in explaining the results.
2nd place: Sean Dougherty
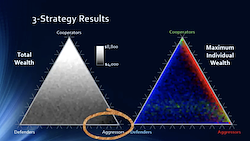 This video clearly explained the challenge, and examined the model that was constructed in NetLogo. It then clearly defined the space of strategies as being based around the notion of cooperative, aggressive, and defensive strategies. The video was able to clearly explain the results of exploring this space and how the different combinations of strategies affected both maximum wealth and average wealth.
This video clearly explained the challenge, and examined the model that was constructed in NetLogo. It then clearly defined the space of strategies as being based around the notion of cooperative, aggressive, and defensive strategies. The video was able to clearly explain the results of exploring this space and how the different combinations of strategies affected both maximum wealth and average wealth.
3rd Place: Mary Bush
 This video not only explained the problem, but also referenced relevant other literature. The submitter also explained how they used a genetic algorithm to explore different strategies by combining some basic strategies, which was a very novel solution. The graphics were useful in explaining this solution. It then explored the results using both total wealth and gini coefficient, and provided some interesting analysis about what strategies were selected for and which strategies were selected against.
This video not only explained the problem, but also referenced relevant other literature. The submitter also explained how they used a genetic algorithm to explore different strategies by combining some basic strategies, which was a very novel solution. The graphics were useful in explaining this solution. It then explored the results using both total wealth and gini coefficient, and provided some interesting analysis about what strategies were selected for and which strategies were selected against.
Honorable Mentions: Smith T. Powell IV, Muhammad Hijazy, Bernhard Geiger, Ronald Paul Ng, Asaf Levi
Spring 2018 Tournament Winners
Click on the winner's name to see their submitted code.
1st Place: Victor Iapascurta
This entry would only ever choose the low or high pool, and never entered the stable pool. To determine which pool to enter it multiplied the payoff of each pool by the number of people in that pool, which for the high pool would be 80 when a quarter of the time and 0 three-quarters of the time, and for the low pool it would 40 half the time and 0 half the time. It then summed these numbers up across the whole run of the model and subtracted the result from 2700. The author explains in the writeup that 2700 is a number chosen to be higher than the expected value of each pool over the course of a 100 round game. If the result of this calculation for the low pool was greater than the high pool it would then enter that pool and vice versa. Essentially this had the effect of always moving to the pool which made less in the past. The author explains in the writeup that there is an expectation over all 100 time steps of what the different pools will generate and hence this solution chooses the pool that has the most potential left. This is an example of the gambler’s fallacy, but potentially works because it is opposite to many of the other strategies which focus on the pools that have paid off the most in the past, while minimizing the number of switches between pools.
2nd Place: Muhammad Hijazy
In this entry, the agent start s in the low pool and stays there for the first 50 rounds of the game. If the sum of the payoffs of the first 50 rounds in the low pool is greater than the sum of the payoffs in the first 50 rounds in the high pool minus the transaction cost tau then it stays in the low pool for the rest of the game, otherwise it switches to the high pool and stays there for the rest of the game. This winds up minimizing switching costs, and also does not rely on the actions of the other agents in the games, which means it works in a wide variety of circumstances.
3rd Place: Ross Grienbenow
This entry starts in the low pool. It then calculates the average number of agents in the low pool and the high pool each round. If the number of agents in both of these pools is greater than 20 on average, it enters the stable pool. Otherwise, using the average number of agents in each of the pools, it calculates an average expected payoff for itself if it had been in the pool it was last in for the entire game. If there are more people on average in the low pool than the high pool and the expected payoff of the low pool is greater than the past payoff that the agent received plus tau, then it switches to the low pool, and vice versa for the high pool. Finally, if the past payoff the agent has received is greater than 1 - tau then it enters the stable pool, otherwise it remains in whatever pool it was in previously. This entry appears to be trying to calculate an expectation of payoffs given the strategies of the other agents in the tournament and then choosing the pool based on the historic choices of the other agents. It was the most complicated agent of all entries, and did particularly well in the mini-tournament where all of the other agents (besides the entries) played a fixed strategy.
4th Place: Sean Dougherty
This entry usually sticks in whatever pool it was last in, but with a probability that decreases as the game goes on it switches to a new random pool with a probability which is biased toward the low and high pools over the stable pool. This entry also does not switch pools often (nearing a zero probability of switching toward the end of the game), and also does not rely on the actions of any of the other agents.
Launch of the Complexity Challenges featured solutions
Watch the video playlist below for visual explanations of solutions submitted in September 2017 for the inaugural Complexity Challenge. The top four submission write ups are available for you to look over as well.